单项选择题
1. 一种货币贬值15%,一年后又增值( )才能保持原币值.
(A)
0.15
(B)
0.152
(C)
0.168
(D)
0.172
(E)
0.176
答案:E
解析:基本公式法 设升值为x,则$\left( {1 - 15\% } \right)\left( {1 + x} \right) = 1$ ∴$x = \frac{3}{{17}} = 0.1756 = 17.65\% $ ∴选E
2. 制鞋厂本月计划生产旅游鞋5000双,结果12天就完成了计划地45%,照这样的进度,这个月(按30天计算)旅游鞋的产量将为( )
(A)
5625双
(B)
5650双
(C)
5700双
(D)
5750双
(E)
5800双
答案:A
解析:基本公式法 每天完成量为:$\frac{{5000 \times 45\% }}{{12}} = \frac{{5000 \times 0.45}}{{12}}$ ∴30天的产量为$\frac{{5000 \times 45\% }}{{12}} \times 30 = 5625$双 ∴选A
3. 一批货物要运进仓库,有甲、乙两队合运9小时,可运进全部货物的50%,乙队单独运则要30小时才能运完,又知甲队每小时可运进3吨,则这批货物共有( )。
(A)
135吨
(B)
140吨
(C)
145吨
(D)
150吨
(E)
155吨
答案:A
解析:基本公式法 甲,乙合运9小时,运进50% $\therefore $运完需要18小时 ∴甲,乙效率为:m甲+m乙=$\frac{1}{{18}}$ 而m乙=$\frac{1}{{30}}$ ∴m甲=$\frac{1}{{18}} - \frac{1}{{30}} = \frac{1}{{45}}$ ∴总货物$\frac{3}{m甲}$ =3×45=135吨 ∴选A
4. 甲、乙两汽车从相距695千米的两地出发,相向而行。乙汽车比甲汽车迟2小时出发,甲汽车每小时行驶55千米,若乙汽车出发后5小时与甲汽车相遇,则乙汽车每小时行驶( )
(A)
55千米
(B)
58千米
(C)
60千米
(D)
62千米
(E)
65千米
答案:D
解析:基本公式法 乙走了5小时,甲走了7小时 ∴7×55+5×V乙=695 ∴V乙=62km/h ∴选D
5. 一元二次不等式$3{x^2} - 4ax + {a^2} < 0(a < 0)$ 的解集是( )
(A)
$\frac{a}{3} < x < a$
(B)
$x > a$或$x < \frac{a}{3}$
(C)
$a < x < \frac{a}{3}$
(D)
$x > \frac{3}{a}$或$x < a$
(E)
$a < x < \frac{3}{a}$
答案:C
解析:基本公式法 $3{x^2} - 4ax + {a^2} < 0$ 等价于$\left( {3x - a} \right)\left( {x - a} \right) < 0$ 因为$a < 0$ ∴$\frac{a}{3} > a$ ∴$a < x < \frac{a}{3}$ ∴选C
6. 设实数x、y适合等式$x{\;^2} - 4xy + 4{y^2} + \sqrt 3 x + \sqrt 3 y - 6 = 0$则x+y的最大值为( )
(A)
$\frac{{\sqrt 3 }}{2}$
(B)
$\frac{{2\sqrt 3 }}{3}$
(C)
$2\sqrt 3 $
(D)
$3\sqrt 2 $
(E)
$3\sqrt 3 $
答案:C
解析:基本公式法 原式变换为:${\left( {x - 2y} \right)^2} + \sqrt 3 x + y = 6$ ∴$\sqrt 3 \left( {x + y} \right) = 6 - {\left( {x - 2y} \right)^2} \le 6$ ∴$x + y \le \frac{6}{{\sqrt 3 }} = 2\sqrt 3 $ ∴选C
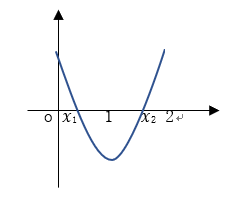
7. 要使方程$3{x^{\rm{2}}} + \left( {m - 5} \right)x + {m^2}\; - m - 2$的两根${x_1},{x_2}$ 分别能满足$0 < {x_1} < 1$和$1 < {x_2} < 2$,实数m的取值范围是( )
(A)
$ - 2 < m < - 1$
(B)
$ - 4 < m < - 1$
(C)
$ - 4 < m < - 2$
(D)
$\frac{{{\rm{ - }}1{\rm{ - }}\sqrt {65} }}{2} < m < - 1$
(E)
${\rm{ - }}3 < m < 1$
答案:A
解析:基本公式法 根据题意可得,此函数开口向上,两根$0 < {x_1} < 1$和$1 < {x_2} < 2$ $f\left( 0 \right) > 0$ ∴ $f\left( 1 \right) < 0$ $f\left( 2 \right) > 0$ 即 ${m^2} - m - 2 > 0$ ${m^2} - 4 < 0$ ${m^2} + m > 0$ ∴$ - 2 < m < - 1$ ∴选A
8. 在四边形ABCD中设AB的长为8, $\angle A:\angle B:\angle C:\angle D = 3:7:4:10$, $\angle CDB = {60^ \circ }$,则△ABD的面积是( )
(A)
8
(B)
32
(C)
4
(D)
16
(E)
18
答案:D
解析:基本公式法 $\angle A:\angle B:\angle C:\angle D = 3:7:4:10$ ∴$\angle A = 360^\circ \times \frac{3}{{24}} = 45^\circ $ $\angle {\rm{B}} = 360^\circ \times \frac{7}{{24}} = 105^\circ $° $\angle {\rm{C}} = 360^\circ \times \frac{4}{{24}} = 60^\circ $ $\angle {\rm{D}} = 360^\circ \times \frac{{10}}{{24}} = 150^\circ $ 因为AB=8, ∴AD=DB=$4\sqrt 2 $ $S = \frac{1}{2} \times 4\sqrt 2 \times 4\sqrt 2 = 16$ ∴选D
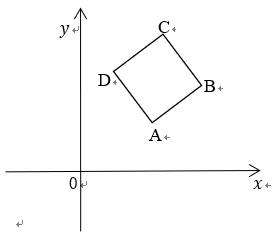
9. 设正方形ABCD如图所示,其中A(2,1),B(3,2),则边CD所在的直线方程是( )
(A)
$y = - x - 1$
(B)
$y = x + 1$
(C)
$y = x - 2$
(D)
$y = 2x + 2$
(E)
$y = - x + 2$
答案:B
解析:基本公式法 A(2,1),B(3,2) ∴C(2,3),D(1,2) ∴CD所在的直线方程为:$\frac{{y - 3}}{{x - 2}} = \frac{{2 - 3}}{{1 - 2}} = 1$ 即:$y = x + 1$ ∴$x + y \le \frac{6}{{\sqrt 3 }} = 2\sqrt 3 $ ∴选B
10. 设AB为圆C的直径,点A,B的坐标分别是(-3,5)(5,1),则圆C的方程是( )
(A)
${\left( {x - 2} \right)^{\rm{2}}}\; + {\left( {y - 6} \right)^{{\rm{2}}\;}} = 80$
(B)
${\left( {x - 1} \right)^{\rm{2}}}\; + {\left( {y - 3} \right)^{\rm{2}}}\; = 20$
(C)
${\left( {x - 2} \right)^{\rm{2}}}\; + {\left( {y - 4} \right)^{\rm{2}}}\; = 80$
(D)
${\left( {x - 2} \right)^{\rm{2}}}\; + {\left( {y - 4} \right)^{\rm{2}}}\; = 20$
(E)
${x^{\rm{2}}}\; + {y^{\rm{2}}}\; = 20$
答案:B
解析:基本公式法 圆心坐标为:AB中点,$x = \frac{{ - 3 + 5}}{2} = 1$, $y = \frac{{5 + 1}}{2} = 3$ ∴选B
11. 圆柱体的底半径和高的比是1:2,若体积增加到原来的6倍,底半径和高的比保持不变,则底半径( )
(A)
增加到原来的$\sqrt 6 $倍
(B)
增加到原来的$\sqrt[3]{6}$ 倍
(C)
增加到原来的$\sqrt 3 $ 倍
(D)
增加到原来的$\sqrt[3]{3}$ 倍
(E)
增加到原来的6倍
答案:B
解析:基本公式法 设原半径为a,高为2a ∴$V = \pi {a^2}2a = 2\pi {a^3}$ 新半径为m,高为2m ∴$6V = 12\pi {a^3} = \pi {m^2}2m = 2\pi {m^3}$ 即${m^3} = 6{a^3}$ ∴$m = \sqrt[3]{6}a$ ∴选B
12. 有3个人,每个人都以相同的概率被分配到4间房的每一间中,某指定房间中恰有2人的概率是( )
(A)
$\frac{1}{{64}}$
(B)
$\frac{3}{{64}}$
(C)
$\frac{9}{{64}}$
(D)
$\frac{5}{{32}}$
(E)
$\frac{3}{{16}}$
答案:C
解析:基本公式法 3个人分配到4个房间,共有:4×4×4=64种 指定房间恰有2人,共有$C_3^2C_3^1$ 所以$P{\rm{ = }}\frac{{C_3^2C_3^1}}{{64}} = \frac{9}{{64}}$ ∴选C
13. 已知a,b,c三数成等差数列,又成等比数列,设$\alpha \beta $是方程$a{x^{\rm{2}}} + bx - c = 0$的两个根,且$\alpha > \beta $,求${\alpha ^{\rm{3}}}\beta - \alpha {\beta ^{\rm{3}}}$ ( )
(A)
$\sqrt 5 $
(B)
$\sqrt 2 $
(C)
$\sqrt 3 $
(D)
$\sqrt 7 $
(E)
$\sqrt {11} $
答案:A
解析:基本公式法 a,b,c既成等差数列,又成等比数列 ∴$a = b = c \ne 0$ ∴$\alpha + \beta = - \frac{b}{a} = - 1,\alpha \beta = - \frac{c}{a} = - 1$ ∴${\alpha ^3}\beta - \alpha {\beta ^3} = \alpha \beta \left( {{\alpha ^2} - {\beta ^2}} \right) = \alpha \beta \left( {\alpha + \beta } \right)\left( {\alpha - \beta } \right)$ $ = \alpha \beta \left( {\alpha + \beta } \right)\sqrt {{{\left( {\alpha - \beta } \right)}^2}} $ $ = \sqrt {{{\left( {\alpha + \beta } \right)}^2} - 4\alpha \beta } = \sqrt {1 + 4} = \sqrt 5 $ ∴选A
14. 甲、乙两选手进行乒乓球单打比赛,甲选手发球成功后,乙选手回球失误的概率为0.3,若乙选手回球成功,甲选手回球失误的概率为0.4,甲选手回球成功,乙选手再次回球失误的概率为0.5,试计算这几个回合中,乙选手输掉1分的概率是( )
(A)
0.36
(B)
0.43
(C)
0.49
(D)
0.51
(E)
0.57
答案:D
解析:基本公式法 P1=0.3(乙第一次失误) P2=0.7×0.6×0.5=0.21(乙第一次成功,甲第二次成功,乙第二次失误) ∴P=0.3+0.21=0.51 ∴选D




