单项选择题
1. 若$a:b = \frac{1}{3}:\frac{1}{4}$,则$\frac{{12a + 16b}}{{12a - 8b}} = $( )
(A)
2
(B)
3
(C)
4
(D)
-3
(E)
-2
答案:C
解析:基本公式法: $a:b = \frac{1}{3}{\rm{\;}}:\frac{1}{4} = 4:3$,令$a = 4$,$b = 3$ ∴$\frac{{12a + 16b}}{{12a - 8b}}{\rm{ = }}\frac{{12 \times 4 + 16 \times 3}}{{12 \times 4 - 8 \times 3}}{\rm{ = }}\frac{{96}}{{24}}{\rm{ = }}4$ ∴选C
2. 设a,b,c为整数,且$|a - b{|^{20}} + |c - a{|^{41}} = 1$,则$|a - b| + |a - c| + |b - c| = $( )
(A)
2
(B)
3
(C)
4
(D)
-3
(E)
-2
答案:A
解析:特值代入法法: ${\left| {a - b} \right|^{20}} + {\left| {c - a} \right|^{41}} = 1$ 令$a = 2$,$b = 1$,$c = 2$ $\left| {a - b} \right| + \left| {a - c} \right| + \left| {b - c} \right| = 1 + 0 + 1 = 2$ ∴选A
3. 以下命题中正确的一个是( )
(A)
两个数的和为正数,则这两个数都是正数.
(B)
两个数的差为负数,则这两个数都是负数.
(C)
两个数中较大的一个其绝对值也较大.
(D)
加上一个负数,等于减去这个数的绝对值.
(E)
一个数的2倍大于这个数本身.
答案:D
解析:基本公式法 两个数和差的正负,与这两个数自身的正负没有关系 ∴A,B全错。 两个正数中,较大的绝对值也大,∴C错 负数的2倍,越来越小,∴E错 ∴选D
4. 一个大于1的自然数的算术平方根为a,则与该数左右相邻的两个自然数的算术平方根分别为( )
(A)
$\sqrt a - 1,\sqrt a + 1$
(B)
a-1,a+1
(C)
$\sqrt {a - 1} ,\sqrt {a + 1} $
(D)
$\sqrt {{a^2} - 1} ,\sqrt {{a^2} + 1} $
(E)
${a^2} - 1,{a^2} + 1$
答案:D
解析:基本公式法 自然数算术平方根为a,则该自然数为a^2 ∴该自然数左边为${a^2} - 1$,右边为${a^2} + 1$ ∴算术平方根为$\sqrt {{a^2} - 1} $,$\sqrt {{a^2} + 1} $ ∴选D
5. 如图,若三角形ABC的面积为1,$\Delta AEC,\Delta DEC,\Delta BED$的面积相等,则三角形AED的面积为( )

(A)
$\frac{1}{3}$
(B)
$\frac{1}{6}$
(C)
$\frac{1}{5}$
(D)
$\frac{1}{4}$
(E)
$\frac{2}{5}$
答案:B
解析:基本公式法 ${S_{\Delta AEC}} = {S_{\Delta DEC}} = {S_{\Delta BED}}$,∴${S_{\Delta BED}} = \frac{1}{3}$ ${S_{\Delta BED}} = {S_{\Delta CED}}$,∴$BD = \frac{1}{2}BC$ ${S_{\Delta ABD}} = \frac{1}{2}$ ${S_{\Delta AED}} = {S_{\Delta ABD}} - {S_{\Delta BED}} = \frac{1}{2} - \frac{1}{3} = \frac{1}{6}$ ∴选B
6. 若以连续掷两枚骰子分别得到的点数a和b作为点M的坐标,则点M落入圆${x^2} + {y^2} = 18$内(不含圆周)的概率是( )
(A)
$\frac{7}{{36}}$
(B)
$\frac{2}{{9}}$
(C)
$\frac{1}{{4}}$
(D)
$\frac{5}{{18}}$
(E)
$\frac{11}{{36}}$
答案:D
解析:基本公式法 连续掷两枚骰子,共有$\left( {a,b} \right) = 6 \times 6 = 36$种 其中落入圆${x^2} + {y^2} = 18$内的有$\left( {1,1} \right),{\rm{\;}}\left( {1,2} \right),\left( {1,3} \right),\left( {1,4} \right),\left( {2,1} \right),\left( {2,2} \right),\left( {2,3} \right),\left( {3,1} \right),\left( {3,2} \right),\left( {4,1} \right)$,共10种。 ∴选D
7. 过点A(2,0)向圆${x^2} + {y^2} = 1$作两条切线AM和AN(见下图),则两切线和弧MN所围成的面积(图中阴影部分)为( )

(A)
$1 - \frac{\pi }{3}$
(B)
$1 - \frac{\pi }{6}$
(C)
$\frac{{\sqrt 3 }}{2} - \frac{\pi }{6}$
(D)
$\sqrt 3 - \frac{\pi }{6}$
(E)
$\sqrt 3 - \frac{\pi }{3}$
答案:E
解析:基本公式法 $S阴影 = 2\left( {{S_{\Delta OAN}} - {S扇形{OPN}}} \right)$ $ = 2\left( {\frac{1}{2} \bullet 1 \bullet \sqrt 3 - \frac{1}{6} \bullet \pi \bullet {1^2}} \right)$ $ = \sqrt 3 - \frac{\pi }{3}$ ∴选E

8. 某同学在解方程$\frac{{ax + 1}}{3} - \frac{{x + 1}}{2} = 1$时,误将式中的x+1看成x-1,得出的解为x=1,那么a的值和原方程的解应是( )
(A)
a=1,x=7
(B)
a=2,x=5
(C)
a=2,x=7
(D)
a=5,x=2
(E)
a=5,x=$\frac{1}{7}$
答案:C
解析:基本公式法 把$x = 1$代入, ${\rm{\;}}\frac{{ax + 1}}{3} - \frac{{x + 1}}{2} = 1$可得:$\frac{{a + 1}}{3} = 1$, ∴$a = 2$ 把$a = 2$代入, ${\rm{\;}}\frac{{ax + 1}}{3} - \frac{{x + 1}}{2} = 1$可得:$\frac{{2x + 1}}{3} - \frac{{x + 1}}{2} = 1$ 可得:$x = 7$ ∴选C
9. 某班同学参加智力竞赛,共有A,B,C三题,每题得0分或得满分.竞赛结果无人得0分,三题全部答对的有1人,答对两题的有15人.答对A题的人数和答对B题的人数之和为29人,答对A题的人数和答对C题的人数之和为25人,答对B题的人数和答对C题的人数之和为20人,那么该班的人数为( )
(A)
20
(B)
25
(C)
30
(D)
35
(E)
40
答案:A
解析:基本公式法 设答对A题有x人次,答对B题有y人次,答对C题有z人次, 由题意可得: $x + y = 29$ $x + z = 25$ $y + z = 20$ ∴$x = 17,y = 12,z = 8$ ∴总计有$17 + 12 + 8 = 37$人次答对 其中三题全对有1人,占$1 \times 3 = 3$人次 两题对有15人,占$15 \times 2 = 30$人次 ∴一题对的人有:$37 - 3 - 30 = 4$人 ∴总人数为:$1 + 15 + 4 = 20$人 ∴选A
10. $|3x + 2| + 2{x^2} - 12xy + 18{y^2} = 0$,则2y-3x=( )
(A)
$ - \frac{{14}}{9}$
(B)
$ - \frac{{2}}{9}$
(C)
0
(D)
$\frac{{2}}{9}$
(E)
$\frac{{14}}{9}$
答案:E
解析:解:基本公式法: 原式等价于 $\left| {3x + 2} \right| + 2{\left( {x - 3y} \right)^2} = 0$ ∴$3{\rm{x}} + 2 = 0$,${\rm{x}} - 3{\rm{y}} = 0$,即${\rm{x}} = - \frac{2}{3}$,$y = - \frac{2}{9}$ ∴$2{\rm{y}} - 3{\rm{x}} = - \frac{4}{9} + 2 = \frac{{14}}{9}$ ∴选E
11. 一批救灾物资分别随16列货车从甲站紧急调到600公里外的乙站,每列车的平均速度为125公里/小时。若两列相邻的货车在运行中的间隔不得小于25公里,则这批物资全部到达乙站最少需要的小时数为( )
(A)
7.4
(B)
7.6
(C)
7.8
(D)
8
(E)
8.2
答案:C
解析:基本公式法 当第16列货车到达乙站,相当于第1列货车多走了$15 \times 25 = 375$(第1列与第16列之间有15个间隔) ∴第1列货车总计走了:$600 + 375 = 975$km ∴$t = \frac{{975}}{{125}} = 7.8$h ∴选C
12. 下列通项公式表示的数列为等差数列的是( )
(A)
${a_n} = \frac{n}{{n - 1}}$
(B)
${a_n} = {n^2} - 1$
(C)
${a_n} = 5n + {( - 1)^n}$
(D)
${a_n} = 3n - 1$
(E)
${a_n} = \sqrt n - \sqrt[3]{n}$
答案:D
解析:基本公式法 等差数列通项公式${a_n}$为关于n的一次函数,即${a_n} = kn + b$ ∴选D
13. 某公司员工义务献血,在体检合格的人中,O型血的有10人,A型血的有5人,B型血的有8人,AB型血的有3人。若从四种血型的人中各选1人去献血,则不同的选法种数共有( )
(A)
1200
(B)
600
(C)
400
(D)
300
(E)
26
答案:A
解析:基本公式法 四种血型各选1人 ∴乘法原理,总共有:$C_{10}^1C_5^1C_8^1C_3^1 = 1200$种。 ∴选A
14. 某班有学生36人,期末各科平均成绩为85分以上的为优秀生,若该班优秀生的平均成绩为90分,非优秀生的平均成绩为72分,全班平均成绩为80分,则该班优秀生的人数是( )
(A)
12
(B)
14
(C)
16
(D)
18
(E)
20
答案:C
解析:特殊技巧法—十字交叉法 优秀 90 80-72=8 4 80 非优秀 72 90-80=10 5 ∴优秀人数为:$36 \times \frac{4}{9} = 16$人 ∴选C
15. 若${y^2} - 2(\sqrt x + \frac{1}{{\sqrt x }})y + 3 < 0$对一切实数x恒成立,则y的取值范围是( )
(A)
1
(B)
2
(C)
1
(D)
3
(E)
2
答案:A
解析:基本公式法 题目等价于:${y^2} + 3 < 2y\left( {\sqrt x + \frac{1}{{\sqrt x }}} \right)$ 即$\frac{{{y^2} + 3}}{{2y}} < \sqrt x + \frac{1}{{\sqrt x }}$ 因为$\sqrt x + \frac{1}{{\sqrt x }} \ge 2$(均值不等式,$a + b \ge 2\sqrt {ab} $) ∴$\frac{{{y^2} + 3}}{{2y}} < 2$ 即${y^2} + 3 < 4\;y$ ${y^2} - 4y + 3 < 0$ ∴$1 < y < 3$ ∴选A
16. $ - 1 < x < \frac{1}{3}$. (1) $|\frac{{2x - 1}}{{{x^2} + 1}}| = \frac{{1 - 2x}}{{1 + {x^2}}}$. (2) $|\frac{{2x - 1}}{3}| = \frac{{2x - 1}}{3}$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:E
解析:基本公式法 对于(1),$\left| {\frac{{2x - 1}}{{{x^2} + 1}}} \right| = \frac{{1 - 2x}}{{1 + {x^2}}}$,∴$2x - 1 \le 0$,即$x \le \frac{1}{2}$,不成立 对于(2),$\left| {\frac{{2x - 1}}{3}} \right| = \frac{{2x - 1}}{3}$,∴$2x - 1 \ge 0$,即$x \ge \frac{1}{2}$,不成立 ∴选E
17. $a{x^2} + bx + 1$与$3{x^2} - 4x + 5$的积不含x的一次方项和三次方项. (1) a:b=3:4. (2) $a = \frac{3}{5},b = \frac{4}{5}$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:B
解析:基本公式法 $\left( {a{x^2} + bx + 1} \right)\left( {3{x^2} - 4x + 5} \right) = 3a{x^4} + 3b - 4a{x^3} + \left( {3 - 4b} \right){x^2} + \left( {5b - 4} \right)x + 5$ ∴ $5b - 4 = 0$ $3b - 4a = 0$ ∴$b = \frac{4}{5},a = \frac{3}{5}$ 对于(1),$a:b = 3:4$,不能得出$b = \frac{4}{5}$,∴不成立 对于(2),显然成立 ∴选B
18. $PQ \cdot RS = 12$. (1) 如图,$QR \cdot PR = 12$. (2) 如图,$PQ = 5$.

(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:A
解析:基本公式法 对于(1),$S = \frac{1}{2}QR \cdot PR = \frac{1}{2}PQ \cdot RS$ ∴$QR \cdot PR = 12 = PQ \cdot RS$,成立 对于(2),$PQ = 5$,条件太少,∴不成立 ∴选A
19. $C_n^4 > C_n^6$. (1) n=10. (2) n=9.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:B
解析:基本公式法 对于(1),$m = 10$,$C_{10}^4 = C_{10}^6$,∴不成立 对于(2),$n = 9$, $C_9^4 = \frac{{9 \times 8 \times 7 \times 6}}{{4 \times 3 \times 2}} = 126$ $C_9^6 = C_9^3 = \frac{{9 \times 8 \times 7}}{{3 \times 2}} = 84$ ∴$C_9^4 > C_9^6$ ∴选B
20. $|1 - x| - \sqrt {{x^2} - 8x + 16} = 2x - 5$. (1) 2
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:C
解析:基本公式法 $\left| {1 - x} \right| - \sqrt {{x^2} - 8x + 16} = \left| {1 - x} \right| - \sqrt {{{\left( {x - 4} \right)}^2}} = \left| {1 - x} \right| - \left| {x - 4} \right|$ 当且仅当$1 - x \le 0$,$x - 4 \le 0$时,即$1 \le x \le 4$时, $\left| {1 - x} \right| - \left| {x - 4} \right| = \left( {x - 1} \right) - \left( {4 - x} \right) = 2x - 5$ 显然,联立(1)与(2)时,$2 < x < 3$在$1 \le x \le 4$范围之内 ∴联合选C
21. ${a_1}{a_8} < {a_4}{a_5}$. (1) $\{ {a_n}\} $为等差数列,且${a_1} > 0$. (2) $\{ {a_n}\} $为等差数列,且公差$d \ne 0$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:B
解析:基本公式法 对于等差数列,${a_1}{a_8} = {a_1}\left( {{a_1} + 7d} \right) = {a_1}^2 + 7{a_1}d$ ${a_4}{a_5} = \left( {{a_1} + 3d} \right)\left( {{a_1} + 4d} \right) = {a_1}^2 + 7{a_1}d + 12{d^2}$ 对于(1),${a_1} > 0$,当$d = 0$时,${a_1}{a_8} = {a_4}{a_5}$, ∴不成立 对于(2),$d \ne 0$, ${\rm{\;}}{a_1}{a_8} < {a_4}{a_5}$,成立 ∴选B
22. ${a_1} = \frac{1}{3}$. (1) 在数列$\{ {a_n}\} $中,${a_3} = 2$. (2) 在数列$\{ {a_n}\} $中,${a_2} = 2{a_1},{a_3} = 3{a_2}$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:C
解析:基本公式法 对于条件(1)${a_3} = 2$,无法得知d或q,不能得出${a_1}$ ,不成立。 对于条件(2):${\rm{\;}}{a_2} = 2{a_1}$,${a_3} = 3{a_2}$,不知道具体数值,不能得出${a_1}$,不成立。 联立(1)(2) ${a_3} = 2$ ${a_2} = 2{a_1}$ ${a_3} = 3{a_2}$ 解得 ${a_2} = \frac{2}{3}$,${a_1} = \frac{1}{3}$ ,成立 ∴选C
23. $\frac{n}{{14}}$是一个整数. (1) n是一个整数,且$\frac{{3n}}{{14}}$也是一个整数. (2) n是一个整数,且$\frac{n}{7}$也是一个整数.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:A
解析:基本公式法 对于(1),$\frac{{3n}}{{14}}$是一个整数,那么n一定是14的倍数,∴$\frac{n}{{14}}$是一个整数 对于(2),$\frac{n}{7}$是一个整数,当$n = 7$时,$\frac{n}{{14}}$显然不是整数,∴不成立 ∴选A
24. 整个队列的人数是57. (1) 甲、乙两人排队买票,甲后面有20人,而乙前面有30人. (2) 甲、乙两人排队买票,甲、乙之间有5人.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:E
解析:基本公式法 联立(1)和(2),但是甲、乙两人的位置并没有确定 ∴无法确定总人数 ∴选E
25. ${x^2}{\rm{ + }}mxy + 6{y^2} - 10y - 4 = 0$的图形是两条直线. (1) m=7. (2) m=-7.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:D
解析:基本公式法 对于(1),$m = 7$时,${x^2} + mxy + 6{y^2} - 10y - 4 = \left( {x + 6y + 2} \right)\left( {x + y - 2} \right) = 0$ ∴$x + 6y + 2 = 0$或$x + y - 2 = 0$,表示两条直线,成立 对于(2),$m = - 7$时, ${x^2} + mxy + 6{y^2} - 10y - 4 = \left( {x - 6y - 2} \right)\left( {x - y + 2} \right) = 0$ ∴$x - 6y - 2 = 0$或$x - y + 2 = 0$,表示两条直线,成立 ∴选D
26. 曲线$a{x^2} + b{y^2} = 1$通过4个定点. (1) a+b=1. (2) a+b=2.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:D
解析:基本公式法 对于(1),$a + b = 1$,当${\rm{a}} = 0$,$b = 1$时,${y^2} = 1$,$y = \pm 1$ 当${\rm{a}} = 1$,$b = 0$时,${x^2} = 1$,$x = \pm 1$ 故定点坐标为$\left( { \pm 1, \pm 1} \right)$共4个定点 对于(2),$a + b = 2$,当${\rm{a}} = 0$,$b = 2$时,$2{y^2} = 1$,$y = \pm \frac{{\sqrt 2 }}{2}$ 当${\rm{a}} = 2$,$b = 0$时,$2{x^2} = 1$,$x = \pm \frac{{\sqrt 2 }}{2}$ 故定点坐标为$\left( { \pm \frac{{\sqrt 2 }}{2}, \pm \frac{{\sqrt 2 }}{2}} \right)$共4个定点 ∴选D
27. ${\alpha ^2} + {\beta ^2}$的最小值是$\frac{1}{2}$. (1) $\alpha $和$\beta $是方程${x^2} - 2ax + ({a^2} + 2a + 1) = 0$的两个实根. (2) $\alpha \beta = \frac{1}{4}$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:D
解析:基本公式法 对于(1),${\rm{\alpha }} + {\rm{\beta }} = 2a$,${\rm{\alpha \beta }} = {a^2} + 2a + 1$,$\Delta = 4{a^2} - 4\left( {{a^2} + 2a + 1} \right) \ge 0$,即$a \le - \frac{1}{2}$ ∴${\alpha ^2} + {\beta ^2} = {\left( {\alpha + \beta } \right)^2} - 2\alpha \beta = 4{a^2} - 4\left( {{a^2} + 2a + 1} \right) = 2\left( {{a^2} - 2a - 1} \right)$ 对称轴为$a = 1$,∴当$a = - \frac{1}{2}$ 时,取最小值 ∴${\alpha ^2} + {\beta ^2}$最小值为$2\left( {\frac{1}{4} + 1 - 1} \right) = \frac{1}{2}$成立 对于(2),${\rm{\alpha \beta }} = \frac{1}{4}$ ${\alpha ^2} + {\beta ^2} \ge 2\alpha \beta = 2 \cdot \frac{1}{4} = \frac{1}{2}$,成立(重要不等式,${a^2} + {b^2} \ge 2ab$) ∴选D
28. 张三以卧姿射击10次,命中靶子7次的概率是$\frac{{15}}{{128}}$. (1) 张三以卧姿打靶的命中率是0.2 (2) 张三以卧姿打靶的命中率是0.5
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:B
解析:基本公式法 对于(1) 命中率0.2 命中7次,∴$p = c_{10}^7{\left( {0.2} \right)^7}{\left( {0.8} \right)^3} = \frac{{120 \times 64}}{{{5^{10}}}}$ 对于(2)命中0.5 命中7次,∴$p = c_{10}^7{\left( {\frac{1}{2}} \right)^7}{\left( {\frac{1}{2}} \right)^3} = \frac{{120}}{{{2^{10}}}} = \frac{{15}}{{128}}$ ∴选B
29. 方程$3{x^2} + [2b - 4(a + c)]x + (4ac - {b^2}) = 0$有相等的实根. (1) a,b,c是等边三角形的三条边. (2) a,b,c是等腰三角形的三条边.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:A
解析:基本公式法 方程$3{x^2} + \left[ {2b - 4\left( {a + c} \right)} \right]x + \left( {4ac - {b^2}} \right) = 0$有相等的实根,即 $\Delta = {\left[ {2b - 4\left( {a + c} \right)} \right]^2} - 12\left( {4ac - {b^2}} \right)$ $ = 4{b^2} - 16b\left( {a + c} \right) + 16{\left( {a + c} \right)^2} - 48ac + 12{b^2}$ $ = 16\left( {{a^2} + {b^2} + {c^2} - ab - ac - bc} \right)$ $ = 8[{(a - b)^2} + {(b - c)^2} + {(a - c)^2}] = 0$ 即$a = b = c$ 对于(1),a,b,c是等边三角形,显然成立 对于(2),a,b,c是等腰三角形,显然不成立 ∴选A
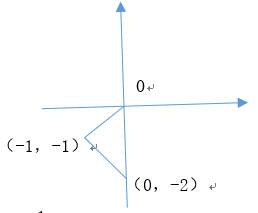
30. 直线$y = x,y = ax + b$与x=0所围成的三角形的面积等于1. (1) a=-1,b=2. (2) a=-1,b=-2.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:D
解析:基本公式法 对于(1),$a = - 1$,$b = 2$,可得: $y = x$ $y = - x + 2$ $x = 0$ 所围成三角形,三点坐标为$\left( {0,0} \right)$,$\left( {0,2} \right)$,$\left( {1,1} \right)$ ∴$S = \frac{1}{2} \times 2 \times 1 = 1$,成立 对于(2),$a = - 1$$b = -2$,可得: $y = x$ $y = - x - 2$ $x = 0$ 所围成三角形,三点坐标为$\left( {0,0} \right)$,$\left( {0,-2} \right)$,$\left( {-1,-1} \right)$ ∴$S = \frac{1}{2} \times 2 \times 1 = 1$,也成立 ∴选D