单项选择题
1. $\frac{{(1 + 3)(1 + {3^2})(1 + {3^4})(1 + {3^8})...(1 + {3^{32}}) + \frac{1}{2}}}{{3 \times {3^2} \times {3^3} \times ... \times {3^{10}}}} = $( )
(A)
$\frac{1}{2} \times {3^{10}} + {3^{19}}$
(B)
$\frac{1}{2} + {3^{19}}$
(C)
$\frac{1}{2} \times {3^{19}}$
(D)
$\frac{1}{2} \times {3^{9}}$
(E)
以上都不对
答案:D
解析:基本公式法 分子分母同乘(3-1) $\frac{{\left( {3 - 1} \right)\left( {3 + 1} \right)\left( {{3^2} + 1} \right)\left( {{3^4} + 1} \right) \cdots \left( {{3^{32}} + 1} \right) + \frac{1}{2} \times \left( {3 - 1} \right)}}{{{3^{1 + 2 + \cdots + 10}}\left( {3 - 1} \right)}}$ $ = \frac{{\left( {{3^2} - 1} \right)\left( {{3^2} + 1} \right) \cdots \left( {{3^{32}} + 1} \right) + 1}}{{{3^{\frac{{10\left( {1 + 10} \right)}}{2}}} \times 2}}$ $ = \frac{{{3^{64}} - 1 + 1}}{{{3^{55}} \times 2}} = \frac{{{3^9}}}{2}$ ∴选D
2. 若三角形ABC的三边a,b,c满足${a^2} + {b^2} + {c^2} = ab + ac + bc$,则三角形ABC为( )
(A)
等腰三角形
(B)
直角三角形
(C)
等边三角形
(D)
等腰直角三角形
(E)
以上都不是
答案:C
解析:基本公式法 $2({a^2} + {b^2} + {c^2}) = 2ab + 2ac + 2bc$ ∴${\left( {a - b} \right)^2} + {\left( {b - c} \right)^2} + {\left( {a - c} \right)^2} = 0$ ∴$a = b = c$ ∴等边三角形 ∴选C
3. P是以a为边长的正方形,${P_1}$是以P的四边中点为顶点的正方形,${P_2}$是以${P_1}$的四边中点为顶点的正方形,${P_i}$是以${P_{i - 1}}$的四边中点为顶点的正方形,则${P_6}$的面积是( )
(A)
$\frac{{{a^2}}}{{16}}$
(B)
$\frac{{{a^2}}}{{32}}$
(C)
$\frac{{{a^2}}}{{40}}$
(D)
$\frac{{{a^2}}}{{48}}$
(E)
$\frac{{{a^2}}}{{64}}$
答案:E
解析:基本公式法 P的边长为$a$,面积为${a^2}$ ${p_1}$的边长为$\frac{{\sqrt 2 }}{2}a$,面积为$\frac{{{a^2}}}{2}$ ${p_2}$的边长为$\frac{a}{2}$,面积为$\frac{{{a^2}}}{4}$ 观察发现,面积为$\frac{1}{2}$的等比数列 ∴${p_6} = {\left( {\frac{1}{2}} \right)^6}{a^2} = \frac{1}{{64}}{a^2}$ ∴选E
4. 某单位有90人,其中65人参加外语培训,72人参加计算机培训,已知参加外语培训而未参加计算机培训的有8人,则参加计算机培训而未参加英语培训的人数是( )
(A)
5
(B)
8
(C)
10
(D)
12
(E)
15
答案:E
解析:文氏图 既参加外语,又参加计算机为65-8=57人 ∴参加计算机未参加英语为72-57=15 ∴选E

5. 方程${x^2} - (1 + \sqrt 3 )x + \sqrt 3 = 0$的两根分别为等腰三角形的腰a和底b(a
(A)
$\frac{{\sqrt {11} }}{4}$
(B)
$\frac{{\sqrt {11} }}{8}$
(C)
$\frac{{\sqrt 3 }}{4}$
(D)
$\frac{{\sqrt 3 }}{5}$
(E)
$\frac{{\sqrt 3 }}{8}$
答案:C
解析:基本公式法 韦达定理:$a + b = 1 + \sqrt 3 $ $ab = \sqrt 3 $ 又因为$b > a$ ∴$b = \sqrt 3 a = 1$ ∴$s = \frac{1}{2} \cdot \sqrt 3 \cdot \frac{1}{2} = \frac{{\sqrt 3 }}{4}$ ∴选C

6. 一辆出租车有段时间的营运全在东西走向的一条大道上,若规定向东为正向,向西为负向.且知该车的行驶的公里数依次为-10,6,5,-8,9,-15,12,则将最后一名乘客送到目的地时该车的位置是( )
(A)
在首次出发地的东面1公里处
(B)
在首次出发地的西面1公里处
(C)
在首次出发地的东面2公里处
(D)
在首次出发地的西面2公里处
(E)
仍在首次出发地
答案:B
解析:基本公式法 -10-8-15+6+5+9+12=-1 ∴向西1公里 ∴选B
7. 如图所示长方形ABCD中的AB=10cm,BC=5cm,设AB和AD分别为半径作半圆,则图中阴影部分的面积为( )

(A)
$25 - \frac{{25}}{2}\pi c{m^2}$
(B)
$25 + \frac{{125}}{2}\pi c{m^2}$
(C)
$50 + \frac{{25}}{4}\pi c{m^2}$
(D)
$\frac{{125}}{4}\pi - 50c{m^2}$
(E)
以上都不是
答案:D
解析:基本公式法 S阴影=S扇$_{ABE}$+S扇$_{ADF}$-${S_{ABCD}}$ $ = \frac{1}{4}\pi {\left( {10} \right)^2} + \frac{1}{4}\pi {\left( 5 \right)^2} = 10 \times 5$ $ = \frac{{125}}{4}\pi - 50$ ∴选D
8. 若用浓度为30%和20%的甲乙两种食盐溶液配成浓度为24%的食盐溶液500克,则甲乙两种溶液各取( )
(A)
180克,320克
(B)
185克,315克
(C)
190克,310克
(D)
195克,305克
(E)
200克,300克
答案:E
解析:基本公式法 十字交叉法 甲30% 4 24% 乙20% 6 ∴甲/乙${\rm{ = }}\frac{4}{6}{\rm{ = }}\frac{2}{3}$ ∴甲200g,乙300g ∴选E
9. 将价值200元的甲原料与价值480元的乙原料配成一种新原料,若新原料每一千克的售价分别比甲、乙原料每千克的售价少3元和多1元,则新原料的售价是( )元.
(A)
15
(B)
16
(C)
17
(D)
18
(E)
19
答案:C
解析:基本公式法 设原料x元,甲x+3元,乙x-1元 ∴$\frac{{200}}{{x + 3}} + \frac{{480}}{{x - 1}}{\rm{ = }}\frac{{680}}{x}$(质量守恒) 可得:x=17 ∴选C
10. 直角边之和为12的直角三角形面积最大值等于( )
(A)
16
(B)
18
(C)
20
(D)
22
(E)
以上都不是
答案:B
解析:基本公式法 $a + b = 12 \ge 2\sqrt {ab} $(均值不等式) ∴$\sqrt {ab} \le 6$ $ab \le 36$ $S = \frac{1}{2}ab \le 18$ ∴选B
11. 如果数列$\{ {a_n}\} $的前n项和${S_n} = \frac{3}{2}{a_n} - 3$,那么这个数列的通项公式是( )
(A)
${a_n} = 2({n^2} + n + 1)$
(B)
${a_n} = 3 \times {2^2}$
(C)
${a_n} = 3n + 1$
(D)
${a_n} = 2 \times {3^n}$
(E)
以上都不是
答案:D
解析:基本公式法 ${S_n} = \frac{3}{2}{a_n} - 3$ ① ${S_{n - 1}} = \frac{3}{2}{a_{n - 1}} - 3$ ② 令①-②得 ${S_n} - {S_{n - 1}} = \frac{3}{2}{a_n} - 3 - \left( {\frac{3}{2}{a_{n - 1}} - 3} \right)$ 即:${a_n} = 3{a_{n - 1}}$ ∴$\frac{{{a_n}}}{{{a_{n - 1}}}} = 3$ 当n=1时,${S_1} = {a_1} = \frac{3}{2}{a_1} - 3$ ∴${a_1} = 6$ 当n=2时,${S_2} = {a_1} + {a_2} = \frac{3}{2}{a_1} - 3$ ∴${a_1} = 6$ ∴$6 + {a_2} = \frac{3}{2}{a_2} - 3$ ${a_2} = 18$ 满足$\frac{{{a_2}}}{{{a_1}}} = 3$ ∴${a_n} = 6 \cdot {3^{n - 1}} = 2 \cdot {3^n}$ 特殊技巧法——特值代入法 当n=1时,${S_1} = \frac{3}{2}{a_1} - 3,{a_1} = 6$ 当n=2时,${S_2} = \frac{3}{2}{a_2} - 3$ ∴${a_1} + {a_2} = \frac{3}{2}{a_2} - 3$ ∴${a_2} = 18$ ∴验证5个选项,只有D满足 ∴选D
12. 以直线y+x=0为对称轴且与直线y-3x=2对称的直线方程为( )
(A)
$y = \frac{x}{3} + \frac{2}{3}$
(B)
$y = - \frac{x}{3} + \frac{2}{3}$
(C)
y=-3x-2
(D)
y=-3x+2
(E)
以上都不是
答案:A
解析:基本公式法 y-3x=2关于y+x=0即y=-x対称 根对称公式x变-y,y变-x 即-x+3y=2 $y = \frac{x}{3} + \frac{2}{3}$ ∴选A
13. 有两排座位,前排6个座,后排7个座.若安排2人就坐.规定前排中间2个座位不能坐.且此2人始终不能相邻而坐,则不同的坐法种数为( )
(A)
92
(B)
93
(C)
94
(D)
95
(E)
96
答案:C
解析:基本公式法 2人在前排,只能1左1右,共有:2×2×2=8种 2人1前1后,共有4×7×2=56种 2人在后排,共有$A_7^2 - 2A_6^1$(2人7位置全排减去2人相邻) =42-12=30种 总计:8+56+30=94种 ∴选C
14. 若从原点出发的质点M向x轴正向移动一个和两个坐标单位的概率分别是$\frac{2}{3}$和$\frac{1}{3}$,则该质点移动3个坐标单位,到达x=3的概率是( )
(A)
$\frac{{19}}{{27}}$
(B)
$\frac{{20}}{{27}}$
(C)
$\frac{{7}}{{9}}$
(D)
$\frac{{22}}{{27}}$
(E)
$\frac{{23}}{{27}}$
答案:B
解析:基本公式法 $P\left( {x = 3} \right) = P\left( {x = 1} \right)P\left( {x = 2} \right) + P\left( {x = 2} \right)P\left( {x = 1} \right) + P\left( {x = 1} \right)P\left( {x = 1} \right)P\left( {x = 1} \right)$ $ = \frac{2}{3} \times \frac{1}{3} + \frac{1}{3} \times \frac{2}{3} + \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} = \frac{{20}}{{27}}$ ∴选B
15. 某乒乓球男子单打决赛在甲乙两选手间进行比赛用7局4胜制.已知每局比赛甲选手战胜乙选手的概率为0.7,则甲选手以4:1战胜乙的概率为( )
(A)
$0.84 \times {0.7^3}$
(B)
$0.7 \times {0.7^3}$
(C)
$0.3 \times {0.7^3}$
(D)
$0.9 \times {0.7^3}$
(E)
以上都不对
答案:A
解析:基本公式法 甲4:1获胜,前4局甲3:1领先 P(甲3:1)=$C_4^3 \times {0.7^3} \times 0.3{\rm{ = }}1.2 \times {0.7^3}$ 第五局甲获胜0.7 ∴p(甲4:1)=$0.7 \times 1.2 \times {0.7^3} = 0.84 \times {0.7^3}$ ∴选A
16. 本学期某大学的a个学生或者付x元的全额学费或者付半额学费,付全额学费的学生所付的学费占a个学生所付学费总额的比率是$\frac{1}{3}$. (1) 在这a个学生中20%的人付全额学费. (2) 这a个学生本学期共付9120元学费.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:A
解析:基本公式法 对于(1),20%付全款,80%付一半 ∴p(全额)$ = \frac{{20\% a}}{{20\% ax + 80\% a \cdot \frac{x}{a}}} = \frac{{0.2}}{{0.2 + 0.4}} = \frac{1}{3}$ 对于(2)与百分比无关 ∴选A
17. 两直线y=x+1,y=ax+7与x轴所围成的面积是$\frac{{27}}{4}$. 17. 两直线y=x+1,y=ax+7与x轴所围成的面积是$\frac{{27}}{4}$. (1) a=-3. (2) a=-2.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:B
解析:基本公式法 对于(1)a=3 ∴$s = \frac{1}{2}\left( {\frac{7}{3} + 1} \right) \times \frac{5}{2} = \frac{5}{4} \times \frac{{10}}{3} = \frac{{25}}{6}$ 对于(2)$a = - 2$ $s = \frac{1}{2}\left( {\frac{7}{2} + 1} \right) \times 3 = \frac{{21}}{4} + \frac{3}{2} = \frac{{27}}{4}$ ∴选B


18. f(x)有最小值2. (1) $f(x) = |x - \frac{5}{{12}}| + |x - \frac{1}{{12}}|$. (2) $f(x) = |x - 2| + |4 - x|$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:B
解析:基本公式法 对于(1),$f{\left( x \right)_{\min }} = \left| {\frac{5}{{12}} - \frac{1}{{12}}} \right| = \frac{1}{3}$ 对于(2),$f{\left( x \right)_{\min }} = \left| {4 - 2} \right| = 2$ ∴选B
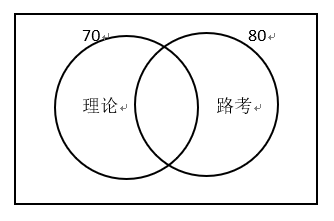
19. 申请驾照时必须参加理论考试和路考且两种考试均通过,若在同一批学员中有70%的人通过了理论考试,80%的通过了路考,则最后领到驾驶执照的人有60%. (1) 10%的人两种考试都没通过. (2) 20%的人仅通过了路考.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:D
解析:基本公式法 对于(1)10%的人都没有过 ∴P(理论)+ P(路考)-P(全过)=90% ∴70%+80%- P(全过)=90% ∴P(全过)=60% 对于(2)仅20%通过了路考 ∴80%-20%=60%的人全部通过了考试 ∴选D
20. ${S_2} + {S_5} = 2{S_8}$. (1) 等比数列前n项的和为${S_n}$且公比$q = - \frac{{\sqrt[3]{4}}}{2}$. (2) 等比数列前n项的和为${S_n}$且公比$q = \frac{1}{{\sqrt[3]{2}}}$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:A
解析:基本公式法 ${S_2} + {S_5} = 2{S_8}\frac{{{a_1}\left( {1 - {q^2}} \right)}}{{1 - q}}$ 即$\frac{{{a_1}\left( {1 - {q^2}} \right)}}{{1 - q}} + \frac{{{a_1}\left( {1 - {q^5}} \right)}}{{1 - q}} = \frac{{2{a_1}\left( {1 - {q^8}} \right)}}{{1 - q}}$ ${q^2} + {q^5} = 2{q^8}$ $2{q^6} - {q^3} - 1 = 0$ $\left( {2{q^3} + 1} \right)\left( {{q^3} - 1} \right) = 0$ ∴${q^3} = - \frac{1}{2}$或$q = 1$(舍去) ${q^3} = - \frac{4}{8}$ 即$q = - \frac{{\sqrt[3]{4}}}{2}$ ∴选A
21. 方程$2a{x^2} - 2x - 3a + 5 = 0$的一个根大于1,另一个根小于1. (1) a>3. (2) a<0.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:D
解析:基本公式法 方程$2a{x^2} - 2x - 3a + 5 = 0$一根大于1,一根小于1 分两种,a>0时,f(1)<0 a<0时,f(1)>0 综上$af\left( 1 \right) < 0$ ∴a<0或a>3 ∴选D
22. 动点(x,y)的轨迹是圆. (1) $|x - 1| + |y| = 4$. (2) $3({x^2} + {y^2}) + 6x - 9y + 1 = 0$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:B
解析:基本公式法 对于(1)$\left| {x - 1} \right| + \left| y \right| = 4$ $x \ge 1,y \ge 0$时,$x - 1 + y = 4$ 即:$x + y = 5$ $x \ge 1,y < 0$时,$x - 1 - y = 4$ 即:$x - y = 5$ $x < 1,y \ge 0$时,$1 - x + y = 4$ 即:$ - x + y = 3$ $x < 1,y < 0$ 时,$1 - x - y = 4$ 即:$ - x - y = 3$ 对于(2)$3\left( {{x^2} + {y^2}} \right) + 6x - 9y + 1 = 0$ 即${x^2} + {y^2} + 2x - 3y + \frac{1}{3} = 0$ ${\left( {x + 1} \right)^2} + {\left( {y - \frac{3}{2}} \right)^2} = \frac{{35}}{{12}}$ 圆心$\left( { - 1,\frac{3}{2}} \right),r = \sqrt {{\textstyle{{35} \over {12}}}} $ ∴选B

23. 一件含有25张一类贺卡和30张二类贺卡的邮包的总重量(不计包装重量)为700克. (1) 一类贺卡重量是二类贺卡重量的3倍. (2) 一张一类贺卡和两张类贺卡的总重量是$\frac{{100}}{3}$克.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:C
解析:基本公式法 联立(1)和(2)设一张一类卡x克,一张二类卡y克 $x + 2y = \frac{{100}}{3}$ $x = 3y$ 可得:$x = 20,y = \frac{{20}}{3}$ ∴$25 \times 20 + 30 \times \frac{{20}}{3} = 500 + 200 = 700$ ∴联合选C
24. a=-4. (1) 点A(1,0)关于直线x-y+1=0的对称点是$A'(\frac{a}{4}, - \frac{a}{2})$. (2) 直线${L_1}:(2 + a)x + 5y = 1$与直线${L_2}:ax + (2 + a)y = 2$垂直.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:A
解析:基本公式法 对于(1),A(1,0)关于x-y+1=0対称 设对称点$A'\left( {{x_0},{y_0}} \right)$,中点$M\left( {\frac{{{x_0} + 1}}{2},\frac{{{y_0}}}{2}} \right)$ 即 $\frac{{{x_0} + 1}}{2} - \frac{{{y_0}}}{2} + 1 = 0$ $\frac{{{y_0}}}{{{x_0} - 1}} = - 1$ 可得:$A'\left( { - 1,2} \right)$ 即:$\frac{a}{4} = - 1,a = - 4$ 对于(2)${l_1}:\left( {2 + a} \right)x + 5y = 1$与${l_2}:ax + \left( {2 + a} \right) \cdot y = 2$垂直 即$\left( {\frac{{2 + a}}{{ - 5}}} \right) \cdot \left( {\frac{{ - a}}{{2 + a}}} \right) = - 1$ $a = - 5$ 或者:当$a = - 2,{l_1}:5y = 1,{l_2}: - 2x = 2$ 也是垂直的 ∴选A
25. 公路AB上各站之间共有90种不同的车票. (1) 公路AB上有10个车站,每两站之间都有往返车票. (2) 公路AB上有9个车站,每两站之间都有往返车票.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:A
解析:基本公式法 对于(1)有10个车站,共有$C_{10}^2A_2^2 = 90$种票 对于(2)有9个车站,共有$C_9^2A_2^2 = 72$种票 ∴选A
26. $(2{x^2} + x + 3)( - {x^2} + 2x + 3) < 0$. (1) $x \in [ - 3, - 2]$. (2) $x \in (4,5)$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:D
解析:基本公式法 对于$2{x^2} + x + 3,\Delta = 1 - 4 \times 2 \times 3 = - 23 < 0$ ∴恒大于0 ∴$\left( {2{x^2} + x + 3} \right)\left( { - {x^2} + 2x + 3} \right) < 0$等价于 $ - {x^2} + 2x + 3 < 0$ ∴x<-1或x>3 显然,对于(1)x∈[-3,-2] (2)x∈(4,5) 都是子集 ∴选D
27. $a{b^2} < c{b^2}$. (1) 实数$a,b,c$满足$a + b + c = 0$. (2) 实数$a,b,c$满足$a < b < c$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:E
解析:基本公式法: 当$a = - 1,b = 0,c = 1$时,同时满足条件(1)和(2) 但是$a{b^2} = c{b^2} = 0$ ∴选E
28. 圆${C_1}:{(x - \frac{3}{2})^2} + {(y - 2)^2} = {r^2}$与圆${C_2}:{x^2} - 6x + {y^2} - 8y = 0$有交点. (1) $0 < r < \frac{5}{2}$. (2) $r > \frac{{15}}{2}$.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:E
解析:基本公式法 ${c_1}:$圆心$\left( {\frac{3}{2},2} \right)$,${r_1} = r$ ${c_2}:{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^4} = 25$,圆心(3,4),${r_2} = 5$ 圆心距:$d = \sqrt {{{\left( {3 - \frac{3}{2}} \right)}^2} + {{\left( {4 - 2} \right)}^2}} = \frac{5}{2}$ 两圆相交:$\left| {{r_2} - {r_1}} \right| \le d \le \left| {{r_2} + {r_1}} \right|$ 即:$\left| {5 - r} \right| \le \frac{5}{2} \le 5 + r$ ∴$\frac{5}{2} \le r \le \frac{{15}}{2}$ 对于(1)$o < r < \frac{5}{2}$,(2)$r > \frac{{15}}{2}$ 显然都不成立 ∴选E
29. $a > b$。 (1) a,b为实数,且${a^2} > {b^2}$。 (2) a,b为实数,且${(\frac{1}{2})^a} < {(\frac{1}{2})^b}$。
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:B
解析:基本公式法 对于(1)${a^2} > {b^2},\left| a \right| > \left| b \right|$。取$a = - 2,b = 0,a < b$ 对于(2),${\left( {\frac{1}{2}} \right)^a} < {\left( {\frac{1}{2}} \right)^b}$,指数函数为减函数(a<1) ∴a>b ∴选B
30. $\frac{{b + c}}{{|a|}} + \frac{{c + a}}{{|b|}} + \frac{{a + b}}{{|c|}} = 1$. (1) 实数a,b,c满足a+b+c=0. (2) 实数a,b,c满足abc>0.
(A)
条件(1)充分,但条件(2)不充分
(B)
条件(2)充分,但条件(1)不充分
(C)
条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
(D)
条件(1)充分,条件(2)也充分
(E)
条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案:C
解析:基本公式法 对于(1),$a + b + c = 0$ $a,b,c$为1正2负,或者2正1负 若1正2负,我们设$a > 0$、$b,c < 0$ ∴$a + b = - c > 0$ $a + c = - b < 0$ $b + c = - a < 0$ ∴$\frac{{a + b}}{{\left| c \right|}}{\rm{ + }}\frac{{a + c}}{{\left| b \right|}} + \frac{{b + c}}{{\left| a \right|}} = 1 + 1 - 1 = 1$ 若2正1负,我们设a,b>0,c<0 ∴a+b=-c>0 a+c=-b<0 b+c=-a<0 ∴$\frac{{a + b}}{{\left| c \right|}}{\rm{ + }}\frac{{a + c}}{{\left| b \right|}} + \frac{{b + c}}{{\left| a \right|}} = 1 - 1 - 1 = - 1$ 对于(2),abc>0 abc为1正2负,或者3正 若1正2负如上, 若3正,则 a+b=-c<0 a+c=-b<0 b+c=-a<0 ∴$\frac{{a + b}}{{\left| c \right|}}{\rm{ + }}\frac{{a + c}}{{\left| b \right|}} + \frac{{b + c}}{{\left| a \right|}} = - 1 - 1 - 1 = - 3$ 单独都不成立 ∴选C




